Antecedentes

La enseñanza de las matemáticas y de las ciencias básicas se enfrenta a retos históricos. En muchos casos, la complejidad de esos desafíos ha superado la eficacia del docente, en parte porque los enfoques tradicionales no logran promover aprendizajes profundos [1]. Factores económicos, socioculturales y de inclusión agravan las problemáticas en los distintos niveles educativos [2], [3]. Para responder a estas dificultades en la formación universitaria, especialmente en las ingenierías, se han explorado enfoques, estrategias y recursos que fortalecen la comprensión conceptual, fomentan el aprendizaje activo y favorecen la transferencia del conocimiento a contextos reales. Este cambio de paradigma se basa en revisiones de metodologías activas en ingeniería [4] y en la teoría del alineamiento constructivo, que ha influido en el diseño curricular por competencias [5]. Desde esta perspectiva se distinguen tres categorías clave: enfoques pedagógicos generales, estrategias didácticas específicas y recursos tecnológicos mediadores.

1. Enfoques pedagógicos generales

Estos enfoques promueven la autonomía del estudiante y la transferencia del conocimiento. El aprendizaje basado en problemas (ABP) busca que los estudiantes apliquen sus conocimientos a situaciones reales o académicas [6]–[9], estimulando la creatividad y el pensamiento crítico. La resolución de problemas desarrolla la comprensión conceptual mediante situaciones que exigen modelado, análisis y toma de decisiones [10], [11]. El aprendizaje colaborativo, por su parte, resalta la construcción social del aprendizaje y fomenta el trabajo en equipo, lo que favorece la retención y la construcción de conocimiento significativo [12].

2. Estrategias didácticas específicas

Estas estrategias operativizan los principios del aprendizaje activo. La instrucción entre pares (Peer Instruction) consiste en formular preguntas conceptuales, debatirlas en pequeños grupos y volver a responder [13], reforzando la comprensión y detectando concepciones erróneas. Las demostraciones interactivas en clase (Interactive Lecture Demonstrations, ILD) combinan predicciones y demostraciones experimentales con discusiones guiadas, propiciando rupturas cognitivas constructivas [14]. Los tutoriales de McDermott son guías de trabajo que llevan al estudiante a construir modelos conceptuales mediante preguntas secuenciadas [15]. El modelado matemático contextualizado integra herramientas matemáticas con la resolución de situaciones reales, permitiendo traducir problemas al lenguaje matemático y validar soluciones [16].

3. Recursos tecnológicos mediadores

Los recursos digitales permiten visualizar y explorar fenómenos matemáticos. Las tecnologías de la información y la comunicación (TIC) facilitan representaciones simbólicas, gráficas y numéricas [17], [18]. Los simuladores y entornos interactivos permiten manipular variables y observar el comportamiento de sistemas en tiempo real. Los sistemas de álgebra computacional (CAS) como Mathematica®, Maple® o MATLAB® centran el esfuerzo en el análisis e interpretación de resultados [18]. Finalmente, plataformas de gestión del aprendizaje como Moodle o Canvas, junto con recursos adaptativos, integran metodologías activas y promueven aprendizaje autónomo y retroalimentación constante [19].

Estas prácticas se desarrollan en un contexto influido por transformaciones pedagógicas y factores sociales, institucionales y políticos. A lo largo del tiempo, reformas curriculares y políticas educativas han impulsado, en mayor o menor medida, la adopción de metodologías activas y la incorporación de tecnologías en el aula. Como resultado, se ha creado un ecosistema didáctico dinámico en constante construcción, en el que la enseñanza de las ciencias básicas va más allá de la transmisión de contenidos y busca desarrollar habilidades, actitudes y formas de pensamiento científico que respondan a los desafíos contemporáneos y a las exigencias del entorno profesional donde se insertan los futuros ingenieros.

La estrategia de simuladores digitales

El uso de simuladores digitales en la enseñanza de las ciencias básicas se ha consolidado como una estrategia eficaz para mejorar la comprensión de fenómenos complejos mediante la interacción con representaciones visuales y dinámicas. Estos entornos permiten a los estudiantes experimentar con variables, visualizar el comportamiento de los sistemas y desarrollar habilidades de análisis sin depender de laboratorios físicos costosos o de difícil acceso. Algunos autores señalan que los simuladores ofrecen un entorno ideal para el aprendizaje basado en el descubrimiento guiado y favorecen la construcción activa del conocimiento [20]. Revisiones más recientes confirman que la integración de simulaciones en entornos educativos mejora el rendimiento académico y el compromiso del estudiante en contextos de ciencia e ingeniería [21].

La adopción de simuladores digitales empezó en programas de posgrado y en universidades con acceso privilegiado a tecnologías computacionales, como lo muestran los desarrollos y primeras aplicaciones de herramientas como MATLAB®, ANSYS® (software de simulación de fluidos), LabVIEW® (entorno de programación gráfica) o PhET® (plataforma de simulaciones interactivas) [22]–[25]. En ingenierías orientadas a la infraestructura tecnológica, como la ingeniería eléctrica, el alto costo de los equipos reales ha motivado el uso de modelos computacionales como alternativa accesible. Este fenómeno es particularmente evidente en instituciones de países con economías emergentes, donde el uso de simuladores permite una formación rigurosa y práctica sin inversiones que a menudo resultan inviables.

Numerosos estudios documentan los beneficios de los simuladores en la educación científica. Se ha destacado que estas herramientas facilitan la apropiación rigurosa de conceptos teóricos complejos [26], analizan la transferencia del conocimiento mediante plataformas interactivas [27] y examinan la eficiencia en el uso de la infraestructura gracias a la virtualización de prácticas [28]. Estas investigaciones coinciden en que el uso didáctico de los simuladores no solo mejora la comprensión conceptual, sino que también democratiza el acceso a experiencias formativas avanzadas, independientemente de los recursos disponibles en cada institución.

Propósito de este trabajo

Este artículo busca divulgar una experiencia metodológica basada en el uso de simuladores digitales como herramienta didáctica para la enseñanza de las matemáticas en carreras de ingeniería. Presenta una propuesta de implementación centrada en el desarrollo y aplicación de un simulador diseñado en MATLAB®, acompañada del análisis de la experiencia de un estudiante que interactuó con la herramienta como parte de una estrategia de aprendizaje autónomo y colaborativo. Se pretende ilustrar las posibilidades pedagógicas del uso de simuladores en el aula e invitar a otros docentes a reflexionar y adaptar esta propuesta a sus contextos, más que establecer una receta universal.

Contexto de aplicación

En la enseñanza de las ciencias básicas en carreras de ingeniería y tecnología es habitual buscar estrategias que fomenten la comprensión profunda de los conceptos teóricos mediante el desarrollo de herramientas digitales. Una de estas estrategias consiste en motivar a los estudiantes a construir programas sencillos que apoyen su aprendizaje, tanto en clase como en tareas complementarias. Dependiendo del problema abordado, el uso de software puede ser indispensable para obtener resultados numéricos o visuales o convertirse en un recurso didáctico poderoso aun cuando existan soluciones analíticas accesibles, ya que el proceso de programación favorece la interiorización de conceptos abstractos.

En este artículo se presenta una experiencia implementada en el curso de ecuaciones diferenciales para estudiantes de segundo semestre de Ingeniería Mecánica Eléctrica (IME) en la Facultad de Ingeniería Electromecánica de la Universidad de Colima. El grupo estaba integrado por 36 estudiantes (34 hombres y 2 mujeres), y el proyecto fue desarrollado por un equipo de dos estudiantes como parte de una estrategia pedagógica que se ha aplicado de forma sistemática en esa asignatura durante los últimos quince años. El objetivo es que los estudiantes diseñen simuladores tipo “caja negra” en MATLAB®, en los que el usuario introduce parámetros definidos y el sistema devuelve gráficos o valores que ayudan a visualizar la solución del problema sin exponer los procedimientos internos.

El procedimiento que siguen los estudiantes inicia con la modelación del problema, que puede tomarse de un libro clásico o ser propuesto por el docente. Una vez definido el modelo general, se parametrizan las constantes y se obtiene una solución analítica simbólica —cuando es posible— utilizando lápiz y papel. A partir de esta solución se desarrolla un código en MATLAB® que implementa el algoritmo y genera los resultados gráficos. Con la herramienta GUIDE® (entorno de desarrollo de interfaces gráficas de usuario), se construye además una interfaz gráfica de usuario (GUI, por sus siglas en inglés Graphical User Interface) que permite introducir los valores de entrada y visualizar los resultados de forma intuitiva, como se muestra en la Figura 1.

Figura 1. Proceso de creación de un simulador desarrollado en clases de ciencias básicas impartidas por el autor.

Este procedimiento se aplica incluso con estudiantes sin experiencia previa en programación. La actividad resulta enriquecedora porque evidencia una transición en la forma en que el conocimiento se construye, integrando no solo contenidos disciplinares, sino también habilidades generales como el trabajo colaborativo, la comunicación y la resolución de problemas. El desarrollo del simulador se organiza a lo largo del semestre como una actividad transversal. Al final del curso se realiza una sesión plenaria en la que cada equipo presenta su simulador. Durante estas sesiones se promueven dinámicas de retroalimentación, como lluvia de ideas, debates dirigidos y coevaluación entre pares, lo que ha favorecido tanto el compromiso de los estudiantes como una mejora continua de la calidad de los proyectos.

Diseño e implementación de un simulador estudiantil: el caso de “Projectile_Motion”

Projectile_Motion es un simulador que hace referencia al movimiento de un proyectil y, como se mencionó, fue el trabajo de clase de un par de estudiantes de ecuaciones diferenciales. El problema original se toma de la sección 4.9 del texto clásico [29]. En él se plantea el tiro parabólico: un proyectil se lanza con una inclinación y una velocidad de salida determinadas y, entre otras cosas, debe determinarse el alcance máximo del proyectil en las direcciones horizontal y vertical.

Se plantea el siguiente sistema desacoplado de ecuaciones diferenciales (ec. 1):

donde x es el alcance horizontal, y es la altura alcanzada, v₀ es la velocidad inicial, θ es el ángulo de lanzamiento, g es la aceleración de la gravedad y t es el tiempo. Resolviendo por separado ambas direcciones y haciendo las sustituciones adecuadas para eliminar la dependencia temporal se obtiene la expresión funcional y = f(x, g, θ, v₀) (ec. 2).

Este resultado es útil para visualizar y analizar gráficamente la trayectoria, pues permite generar una gráfica en el plano x–y donde ambas variables dependen del lanzamiento.

Una vez obtenido el modelo y su solución, se implementa el código en MATLAB®. La Figura 2 muestra detalles de diferentes secciones del código.

Figura 2. Detalle de diferentes secciones del código en MATLAB®.

De manera paralela al desarrollo del modelo matemático y su implementación computacional, se desarrolló la interfaz gráfica de usuario (GUI) utilizando el entorno GUIDE®. Para la versión final del simulador que se presentó en clase se acordó un diseño con funcionalidades clave, descritas en la Tabla 1.

Tabla 1. Características funcionales del simulador

Sección	Función
Condiciones iniciales	Permite al usuario ingresar los parámetros de simulación (velocidad, ángulo, posición inicial, etc.).
Plano x–y	Genera la gráfica de la trayectoria resultante del proyectil.
Resultados	Además de la gráfica, muestra los valores del alcance máximo en las direcciones horizontal y vertical.
Botones de acción	Incluyen funciones para graficar la trayectoria, borrar los resultados o generar automáticamente parámetros aleatorios para la simulación.
Ayuda	Ofrece una descripción concisa del objetivo del simulador y del proceso simplificado de resolución analítica.
Documentación adicional	Proporciona enlaces a recursos audiovisuales complementarios y acceso al repositorio del curso con las notas y materiales temáticos.

Una extensión funcional permite modificar el valor de la aceleración de la gravedad para simular el experimento no solo en la Tierra, sino también en otros cuerpos del sistema solar. Para ello se incluye una sección específica donde el usuario puede seleccionar el planeta sobre el cual se realizará la simulación. Las Figuras 3 y 4 muestran aspectos del proceso de diseño de la interfaz gráfica, tanto en su etapa de construcción como en su versión final.

Figura 3. Área de diseño gráfico de la GUI, vacía por defecto.

Figura 4. Diseño final de la GUI con los elementos necesarios para ser usada como recurso educativo digital.

Para ilustrar el uso de la herramienta, las Figuras 5, 6 y 7 muestran los resultados de una simulación, el menú de ayuda y la sección para obtener más recursos audiovisuales.

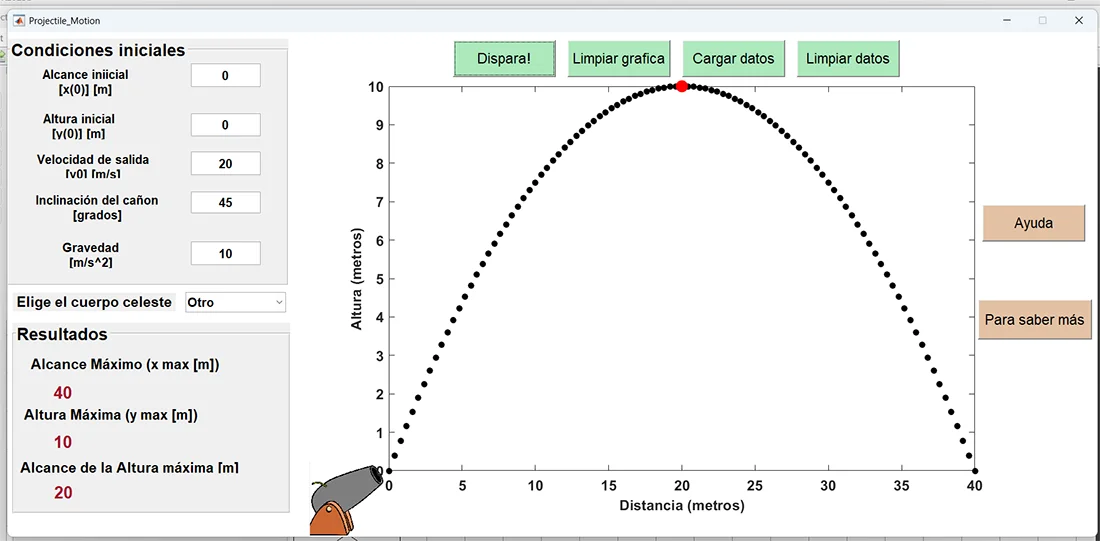
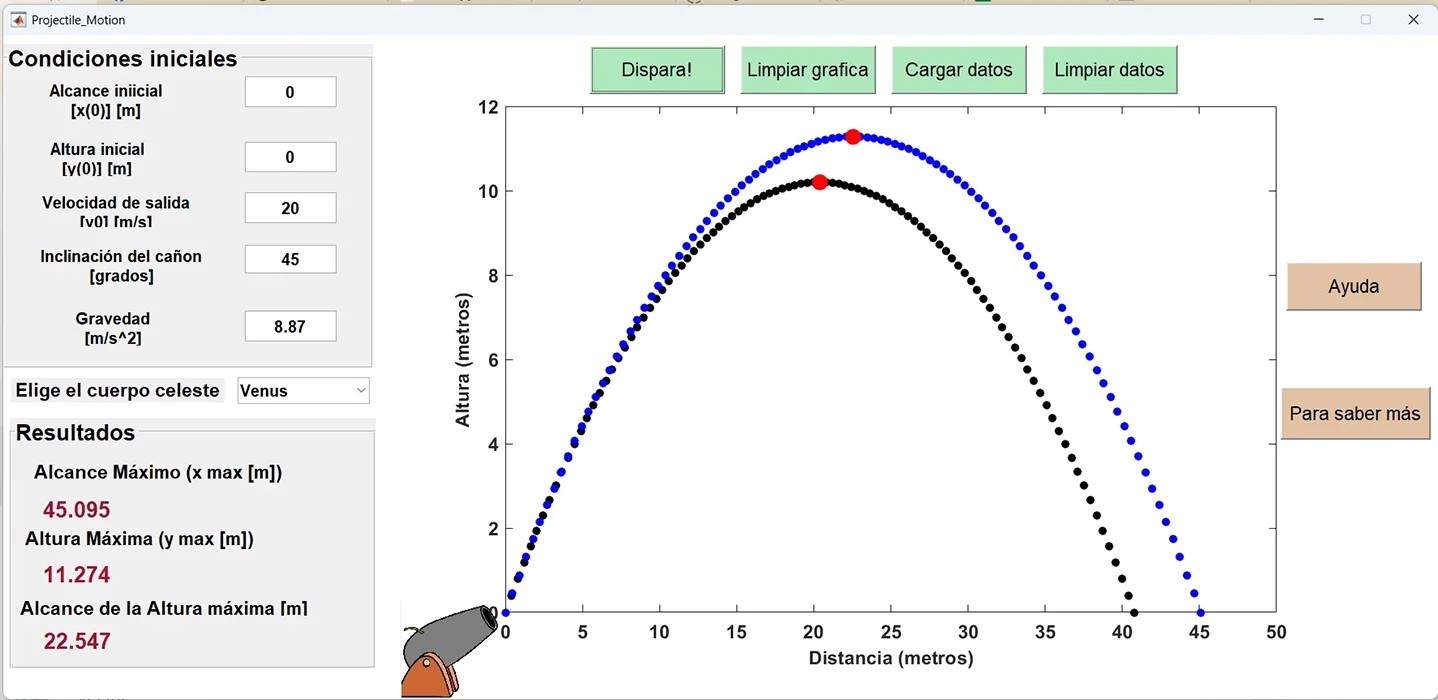
Figura 5. a) Resultados de una simulación realizada. b) Comparación de dos casos.

Figura 6. Menú de ayuda con la fundamentación y solución del problema analítico.

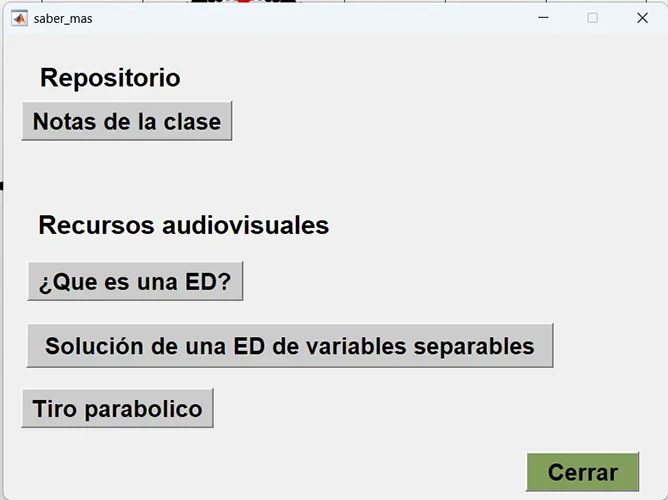
Figura 7. Menú para obtener recursos educativos adicionales.

Impacto del simulador en el aprendizaje: experiencia y rendimiento de los estudiantes

El simulador, junto con sus menús de ayuda y elementos complementarios, constituye un recurso educativo digital (RED) porque es un material en formato digital que facilita y enriquece la experiencia educativa, promoviendo el aprendizaje de manera interactiva y accesible.

Esta herramienta no solo sistematiza la resolución de un problema general; también invita al estudiante a construir conocimientos adicionales, fomentando un aprendizaje profundo y significativo. Al permitir la realización de múltiples experimentos mediante ajustes ilimitados en los datos de entrada, los resultados pueden organizarse en forma tabular o gráfica, lo que facilita su análisis y comprensión. Estas funcionalidades surgen en la etapa de pruebas, ya que las dudas generadas por la variabilidad de los resultados llevan al estudiante a replantearse si el simulador responde correctamente al problema y si la forma de presentar los resultados es la más adecuada.

A menudo se solicita al estudiante que reflexione sobre las capacidades de uso del simulador y se le anima a generar la documentación necesaria para su correcta utilización. Esta práctica permite trabajar diversos aspectos del desarrollo académico, como la capacidad de síntesis, al observar cómo el alumno realiza suficientes simulaciones para identificar escenarios generalizados que luego contextualiza. En algunos casos, el estudiante logra transferir este conocimiento a otras asignaturas del plan de estudios, ampliando así su comprensión y habilidades.

La implementación de este y otros desarrollos en colaboración con los estudiantes ha demostrado proporcionarles un notable sentido de logro. Esta experiencia les permite abordar las matemáticas desde múltiples enfoques, enriqueciendo su aprendizaje con conocimientos adicionales. Estos hallazgos se derivan de una observación sistemática realizada durante más de una década, apoyada en productos entregables como manuales técnicos, informes, presentaciones, rúbricas de evaluación y, en años recientes, ejercicios de autoevaluación y coevaluación. Aunque este artículo no pretende realizar un análisis estadístico formal, se han recogido datos cuantitativos representativos que respaldan las observaciones previas. La Tabla 2 muestra resultados agregados correspondientes a distintos ciclos escolares que permiten identificar patrones de participación, desempeño académico y habilidades desarrolladas por los estudiantes en torno al uso del simulador.

Tabla 2. Datos cuantitativos sobre el impacto de la actividad en el rendimiento del estudiante

Indicador	Clase 2023	Clases 2014–2022
Equipos formados e integrantes	18 equipos de 2 personas	93 equipos con promedio de 4,4 integrantes
Tiempo invertido en la actividad	1 mes	1,4 meses
Equipos con proyectos sobresalientes	4 de 18	12 de 93
Alumnos que concluyeron el simulador	34 de 36 (94,4 %)	339 de 351 (96,6 %)
Calificación promedio obtenida en esta actividad	89,7 %	86,9 %

Indicador	Clase 2023	Clases 2014–2022
Calificación en evaluación escrita de alumnos que no superaron el 80 % de la calificación en el simulador	35,6 %	30,9 %
Calificación en evaluación escrita de alumnos que superaron el 80 % de la calificación en el simulador	60,9 %	58,6 %
Calificación promedio obtenida por el grupo	81,0 %	80,3 %
Autoevaluación y coevaluación *	94,3 %	95,6 %

Fuente: datos históricos de los cursos impartidos por el autor.
* Dato disponible a partir de 2020.

Conclusión

La experiencia acumulada en el desarrollo e implementación de este tipo de actividades permite afirmar que los simuladores digitales pueden tener un impacto significativo en el aprendizaje dentro del aula de ciencias básicas, tanto a nivel conceptual como en el desarrollo de habilidades transversales.

• Los estudiantes manifiestan un notable sentido de logro y satisfacción personal, en especial al completar una tarea que inicialmente perciben como compleja y, en algunos casos, al presentar sus simuladores en ferias profesiográficas o foros técnico científicos.
• Las calificaciones obtenidas en esta actividad tienden a ser altas, ya que la mayoría cumple con los requisitos evaluativos y alcanza los puntajes esperados, contribuyendo así al desempeño general en la asignatura.
• Se promueven competencias adicionales como el trabajo colaborativo, el diseño de cronogramas, la documentación técnica, la comunicación académica y la capacidad de análisis gráfico, todas relevantes en la formación de ingenieros.

Desde la perspectiva docente, esta estrategia se ha mantenido en evolución durante más de quince años. Su implementación ha permitido desarrollar una dinámica pedagógica activa y significativa, con efectos positivos observados en múltiples generaciones de estudiantes. Se reconoce que existen áreas de mejora, particularmente en la sistematización de los instrumentos de evaluación. Aunque en distintas cohortes se han utilizado encuestas, formularios de percepción y ejercicios de autoevaluación y coevaluación, su aplicación no ha sido continua ni con fines comparativos estandarizados.

Por esta razón, aunque el enfoque de evaluación se ha basado principalmente en evidencias de desempeño observable —como la funcionalidad del simulador, la claridad de los informes, la capacidad de análisis y la relación con los resultados en pruebas escritas—, se considera valioso incorporar en futuras ediciones instrumentos validados que complementen este enfoque. Entre ellos podrían incluirse herramientas centradas en el aprendizaje conceptual (por ejemplo, la ganancia de Hake) o encuestas estandarizadas sobre colaboración y uso de tecnología.

Finalmente, aunque esta estrategia ha demostrado su viabilidad técnica y didáctica en el aula, su potencial podría ampliarse mediante proyectos de colaboración multidisciplinaria que integren habilidades avanzadas en computación, diseño instruccional y análisis educativo. Este horizonte no solo enriquecería la calidad de los simuladores, sino también su utilidad como herramientas transferibles a otras áreas del currículo de ingeniería.

Referencias