Introducción

Estamos acostumbrados a observar fenómenos y objetos que se encuentran dentro de nuestras escalas de tiempo y espacio. Para explorar otras escalas, necesitamos extender nuestros sentidos mediante dispositivos tecnológicos. Por ejemplo, usamos telescopios para ver objetos muy lejanos y microscopios para observar objetos muy pequeños. Cuanto más nos alejamos de nuestra escala de observación, más desafiante se vuelve estudiar un fenómeno. Diferentes técnicas de observación y equipos de laboratorio ofrecen distintas resoluciones espaciales y temporales. La resolución espacial se refiere al nivel de detalle con el que se puede distinguir la estructura de un objeto en el espacio, mientras que la resolución temporal se refiere a la capacidad de medir cambios a lo largo del tiempo. Algunas técnicas pueden ver lo muy pequeño, pero carecen de buena resolución temporal, mientras que otras tienen una excelente resolución temporal pero no espacial. Los microscopios electrónicos y de fuerza atómica ofrecen una impresionante resolución espacial, pero no temporal.

Hay sistemas de partículas microscópicas que se mueven muy rápido. En estos casos, sería ideal una técnica de observación con excelentes resoluciones tanto temporales como espaciales, lo cual representa un desafío tecnológico. Un ejemplo son las partículas Brownianas [1-2]. El movimiento Browniano es el movimiento aleatorio de partículas suspendidas en un fluido (líquido o gas) debido a su colisión con las moléculas del fluido. Este movimiento puede describirse en dos regímenes: el régimen difusivo, que se da en escalas de tiempo más largas donde las partículas se mueven aleatoriamente, y el régimen balístico, que se da en escalas de tiempo muy cortas donde las partículas aún no han sido desviadas por colisiones. Lo más avanzado ha sido estudiar una sola partícula Browniana a tiempos muy cortos, usando una técnica de interferometría óptica, que es una técnica basada en la interferencia de ondas de luz para medir pequeñas distancias o cambios en la posición con alta precisión. Estudiar un sistema compuesto por muchas partículas Brownianas, como los cristales coloidales, es un gran reto tecnológico.

Estudiar procesos a nivel molecular en fluidos es aún más difícil. Las moléculas son más pequeñas y rápidas que las partículas Brownianas. Para estos sistemas, se utilizan técnicas de dispersión de ondas electromagnéticas, donde se hace pasar un haz a través del material y se observa la respuesta. Esto permite relacionar la respuesta del material con el orden y dinámica de las partículas, pero solo de manera promediada, sin detalles temporales a nivel de partículas individuales. Conocer el movimiento a este nivel nos ayudaría a responder preguntas como: ¿Cómo se forma un cristal a partir de un líquido? ¿Por qué algunos materiales no cristalizan? Sin embargo, esto no es fácil debido a la cantidad y velocidad de las moléculas antes de formar un sólido.

En este contexto, los métodos que describen fenómenos a nivel de partículas individuales son cruciales. Las simulaciones numéricas ofrecen esta posibilidad y han contribuido significativamente al entendimiento de fenómenos físicos microscópicos. Cuanto más preciso sea nuestro modelo, mejores serán los resultados. Sin embargo, a veces es imposible considerar todos los factores de un fenómeno natural en una simulación, ya sea por su número o por desconocer cómo modelarlos.

Existen sistemas macroscópicos de materia granular fluidizada, donde el movimiento de cada partícula es similar al de coloides (suspensiones de partículas finamente divididas en un medio) o moléculas, pero en una escala de tiempo mayor. La materia granular fluidizada se refiere a un conjunto de partículas sólidas que, cuando se someten a un flujo de gas o líquido, se comportan de manera similar a un fluido. Estas características permiten estudiar estos sistemas con técnicas estándar de videomicroscopía. Cuando decimos que el movimiento de partículas granulares es similar al de las Brownianas o moléculas, nos referimos a que presentan características matemáticamente similares.

A continuación, describimos un sistema granular cuya fluidización se logra mediante un campo magnético alternante. Hemos usado este sistema para modelar la transición vítrea (cambio de un líquido a un estado sólido sin formación de un patrón cristalino), la cristalización (proceso de formación de un sólido ordenado a partir de un líquido) y la formación de vórtices (movimientos circulares de las partículas).

Experimento

Figura 1. El arreglo experimental consiste en un par de bobinas en un arreglo de Helmholtz. Las partículas magnéticas se colocan en un recipiente en el centro del arreglo de bobinas.

En nuestros experimentos, usamos partículas magnéticas de 1 mm de diámetro en un campo magnético alternante con una amplitud máxima de 0 a 100 Gauss. El campo es producido por un par de bobinas en configuración de Helmholtz (un tipo de bobina electromagnética para generar un campo magnético uniforme), alimentadas por un amplificador de potencia controlado por un programa en LabView. Las partículas magnéticas rotan para alinearse con el campo magnético y ruedan sobre la base del recipiente describiendo trayectorias complejas similares a las de partículas Brownianas o activas, como bacterias, dependiendo de la frecuencia aplicada. El sistema funciona en un rango de 0 a 30 Hz. A mayores frecuencias, las partículas no responden con movimiento al campo magnético. Las partículas se mueven por toda la celda. Para caracterizar dinámicamente su movimiento, se determina su desplazamiento cuadrático medio (medida de la media de las distancias recorridas al cuadrado por las partículas) y su coeficiente de difusión (medida de la rapidez con la que las partículas se dispersan). Para caracterizar la estructura formada por muchas partículas, se usa el parámetro orientacional de sexto orden (una medida del orden en la disposición de las partículas). Estas cantidades se complementan para describir el sistema. En la Fig. 2 se observan diferentes trayectorias de una sola partícula a distintas frecuencias. A 2 Hz, el movimiento es aleatorio, mientras que a 19 Hz es persistente. Así, cambiando la frecuencia, podemos modelar diferentes formas de movimiento, desde el Browniano hasta el de materia activa.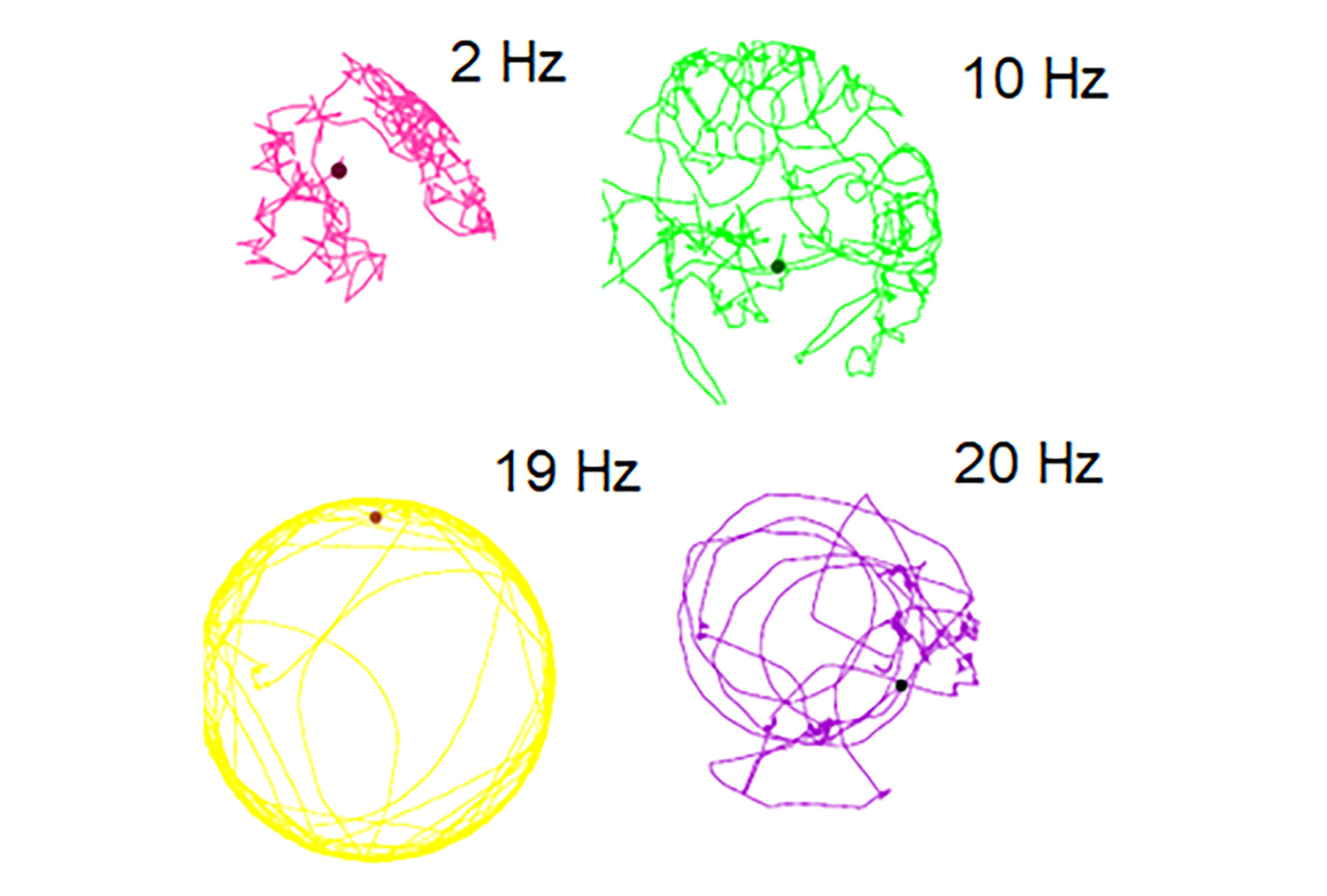

Figura 2. Diferentes trayectorias para diferentes frecuencias. Nótese la diferencia cualitativa de las trayectorias para diferentes frecuencias.

Cristales

Colocando las partículas en una superficie cóncava, tienden a irse al centro, fomentando la agregación. Las partículas poseen energía cinética y tienden a desordenarse. A altas temperaturas, se mueven por todo el recipiente y no se agregan. El confinamiento suave del recipiente no se manifiesta. Si el sistema se enfría gradualmente, puede solidificarse. Al disminuir la temperatura, las partículas se concentran en el centro. Si la temperatura desciende rápidamente, el arreglo final es desordenado, obteniendo vidrios. Si el enfriamiento es lento, se forma un cristal. A enfriamientos intermedios se obtienen policristales. Estos sistemas ayudan a describir el proceso de cristalización.

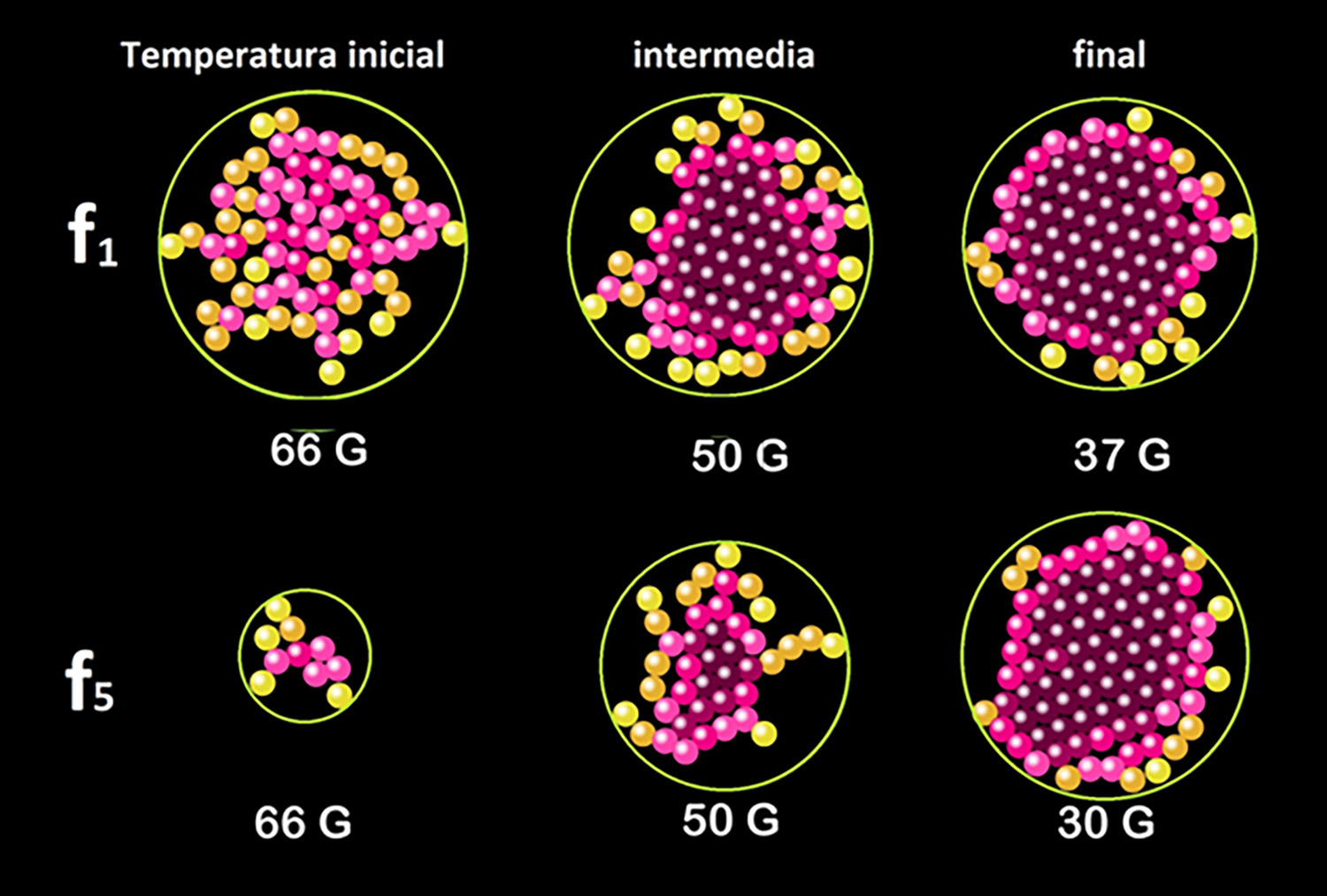
Figura 3. Diferentes arreglos cristalinos obtenidos para dos superficies con diferente concavidad. En ambos casos se forma el núcleo en dos pasos y se observa el paso inicial amorfo.

Estudios teóricos proponen una teoría de nucleación en dos pasos, pero hay pocos experimentos que la comprueben [3-5]. Usando este sistema granular, hemos mostrado evidencia experimental de nucleación en dos pasos. En el primer paso, se forma un agregado desordenado que luego se ordena, formando un núcleo, en contraste con la teoría clásica que describe la nucleación en un solo paso. En la Fig. 3 se observa la evolución de dos cristales en dos superficies parabólicas; en ambos casos se observó nucleación en dos pasos. En el caso de mayor concavidad, f1, el agregado inicial es más grande que en la concavidad menor f5. El estudio de experimentos bajo diferentes condiciones podría determinar cuándo ocurre la nucleación en dos pasos o en uno solo [6-7]. Además, ayuda a comprender el papel del protocolo de enfriamiento en la cristalización. Experimentos preliminares indican que un enfriamiento escalonado es más eficiente que uno lineal, y se puede abordar el papel del confinamiento en la rapidez de cristalización.

Efectos del confinamiento

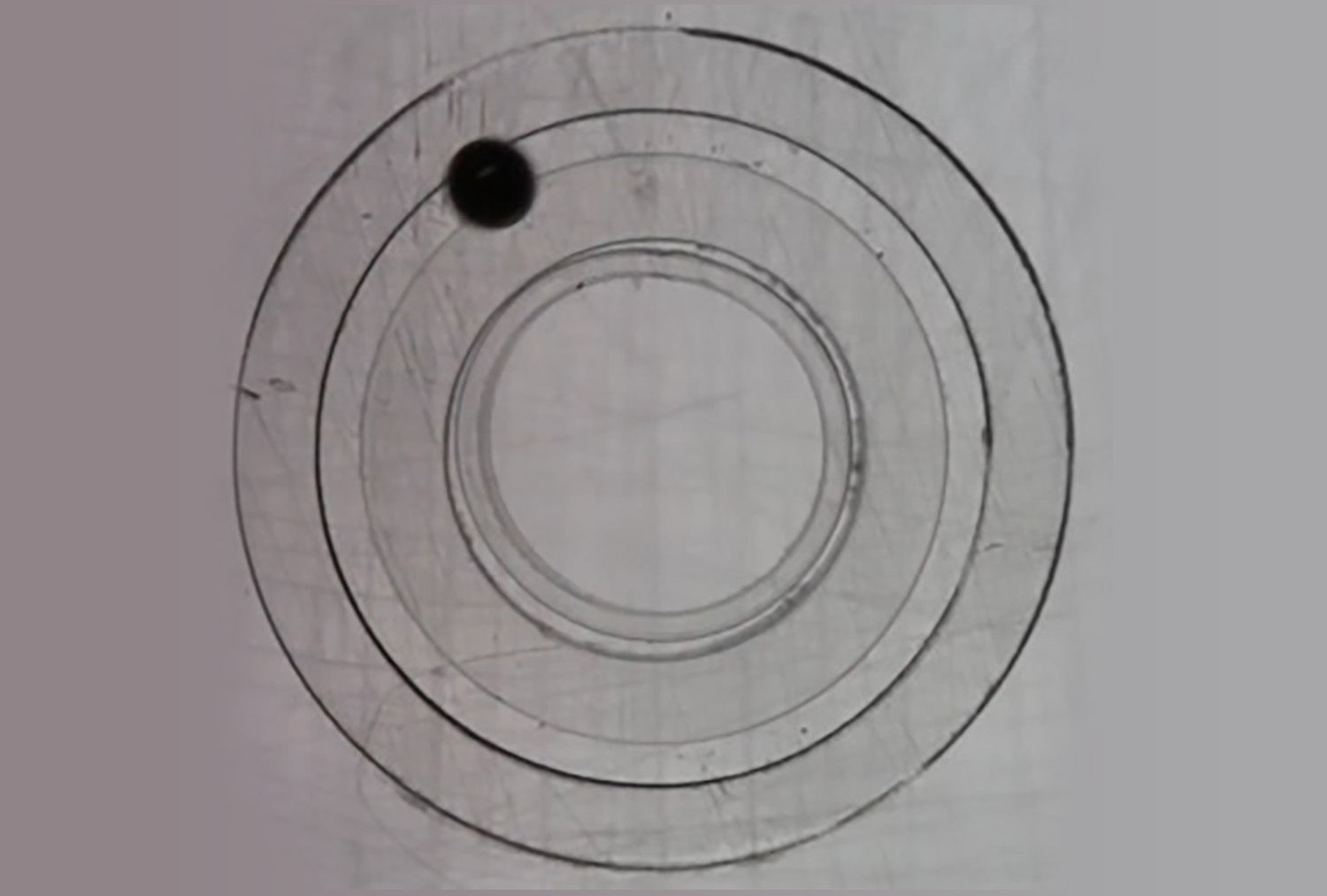
Figura 4. Partícula altamente confinada en una trayectoria circular. Se observa un movimiento más persistente.

La partícula puede ser confinada en una trayectoria curva, como se observa en la Fig. 4. Se ha encontrado que, conforme la partícula está más confinada, los efectos de persistencia en el movimiento se observan más claramente. La trayectoria va en una dirección durante varios ciclos del campo y luego puede cambiar. Los experimentos a nivel de partículas Brownianas son difíciles, pero con nuestro modelo macroscópico solo es necesario obtener los canales de confinamiento, hechos de acrílico con técnica de corte láser.

Figura 5. Formación de vórtices coexistiendo con una fase sólida.

Bajo ciertas condiciones, se da la formación de vórtices que giran en direcciones opuestas. En la Fig. 5 se observa un vórtice en el sistema granular. Conociendo las posiciones de cada partícula, se pueden calcular diferentes cantidades. Así, describimos fenómenos colectivos a nivel de partículas individuales. Nótese las regiones formadas: el vórtice en la parte superior y partículas confinadas en la inferior.

Conclusiones

El sistema descrito es ideal para estudiar procesos en sistemas-modelo de fluidos y sistemas Brownianos. Aunque hay diferencias con sistemas reales, algunos resultados son interesantes. Los resultados fortalecen el uso de modelos macroscópicos para estudiar fluidos y sistemas Brownianos. Se aprovechan los tiempos de relajación accesibles a técnicas de vídeo estándar. El sistema es simple y puede modificarse para modelar otros procesos. Otros sistemas macroscópicos también se han usado para modelar sistemas microscópicos. Recomendamos el uso de sistemas macroscópicos por las posibilidades que ofrecen para profundizar y complementar la descripción física de fenómenos microscópicos.

Referencias